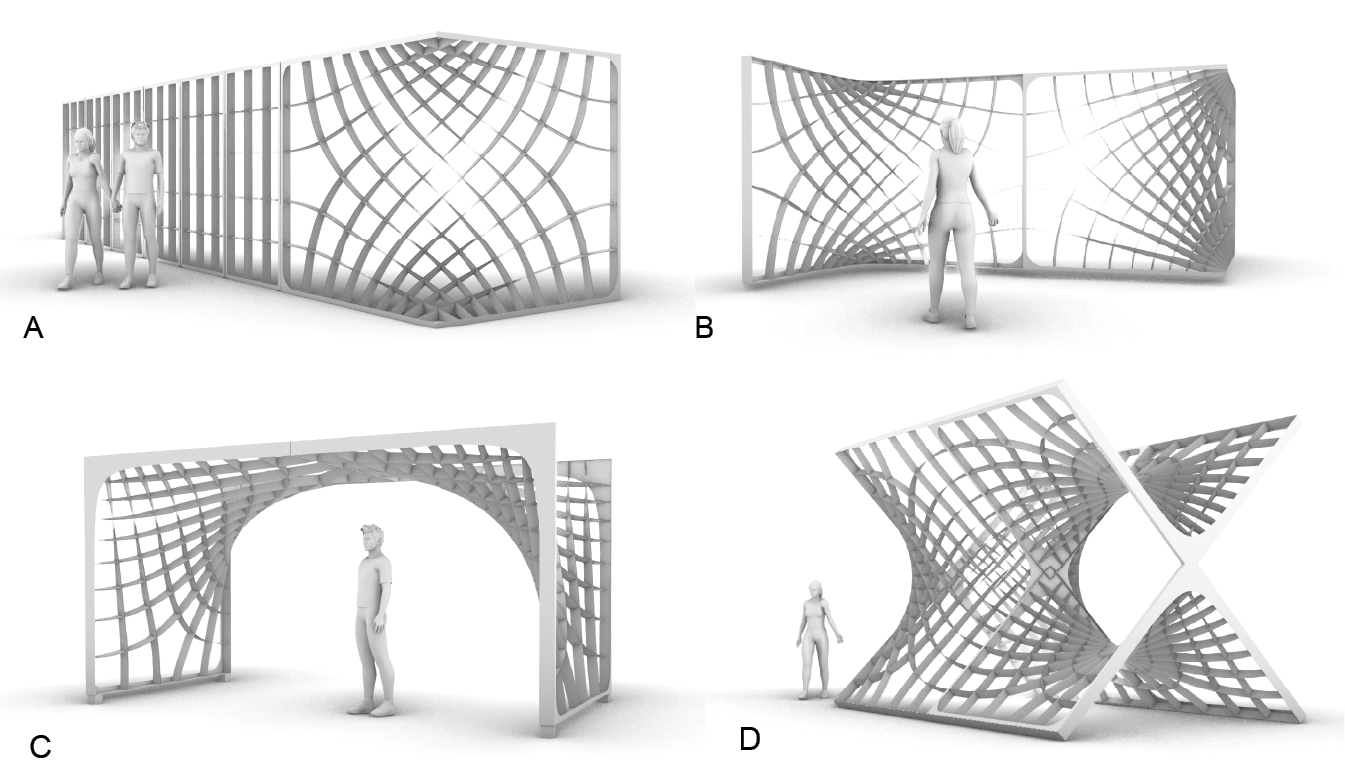
Asymptotic Building Envelope

Eike Schling, Muye Ma, Chih-Lin Hsu (Hong Kong, 2021)

This research project proposes a novel design and construction system for doubly curved curtain wall systems. A full-scale prototype of a 2.4 x 2.4 x 2.4 m corner façade module was constructed at the campus of HKU as well as NTUST (Taiwan). This substructure will be used for testing of structural performance and doubly curved cladding strategies throughout the academic year.There is an urgent need for innovative building construction methods that combine high structural efficiency with low production cost, offer design freedom and integrate well into the built environment. This project is focused on a particular network along the Asymptotic Curves (following the path of vanishing normal curvature). Such a layout can be fabricated from straight and flat elements with repetitive orthogonal nodes. Both laser-cutting and shipping benefit greatly from the straight geometry of lamellas, creating almost no offcuts of the rectangular stainless steel sheet material and minimal packing size.The lamellas are prefabricated and assembled into a flat grid. The slender profiles allow for a simple, self-forming erection process, where the weak axis of the lamellas is elastically bent and twisted to form the design shape, while the strong axis creates high resilience against external loads. The completed curved grid combines the structural benefits of a grillage (local bending moments) and a gridshell (global distribution of forces through tension and compression).Our design is based on a Scherk minimal surface, which is inscribed in a cube. It can be positioned as a corner module into any rectangular building type but also combined to create multiple architectural scenarios, in which modules tie smoothly into one another or even create a periodic minimal surface network. We take advantage of the minimal surface geometry to create an isothermal web, a layout in which all cells are almost quadratic, the substructure follows the asymptotic curves and the diagonals follow the principal curvature directions. Combining these two networks allows us to benefit from their distinct geometric properties for both substructure and façade.Our ongoing research focuses on cladding strategies that take advantage of this layout. In particular, the principal curvature directions allow for planar quad glass panels and elastic developable strips, which can be produced simply and efficiently from flat sheet material. This construction system offers a simplification of both fabrication and construction procedures for substructure and cladding. At the same time, the design is able to create transitions from flat to curved geometry and allows smooth integration into existing curtain wall systems. We anticipate taking advantage of these properties to enhance existing façade structures.

Project credits: Academic Partner: National Taiwan University of Science and Technology (NTUST), Shen Guan Shih. Industry Partner: GOMORE Building Envelope Technology, Chih-Lin Hsu. Project Team: Eike Schling, Jacky Chu, Muye Ma, Wesley She, Fai Lam Chung, Nuozi ChenLee Chun Ki, Yao Dongni, Choi Chung Hei, Chung Bing Tsun, Ma Chun Hon, Ng Sherene Poh Li, So Cheuk Lam, Wang Xiangning, Zhu Xiang, Yang Mei, Chan Ching Yee. Website: www.arch.hku.hk/research_project/asymptotic-building-envelope.

*The substructure was completed in November 2020, and is currently used to test various cladding strategies.*

*The asymptotic network is based on a Scherk minimal surface, creating distinct qualities, such as two singularities (pentagons) at the left and right boundaries.*

*The star connector complete the orthogonal joints while allowing for a curvilinear geometry of lamellas.*

The geometry is related to the rulings of hyperbolic paraboloids, which have been used in architectural construction for over a century by architects and engineers such as Vladimir Shukhov, Felix Canedla, Alvaro Dieste, Le Corbusier and Antonio Gaudi. Asymptotic Curves, however, extend the possibilities to design any negatively curved surface, use repetitive orthogonal joints and create isothermal layouts in combination with principal curvature networks.

*The Asymptotic Structure has the ability to transition from a regular orthogonal grid into a doubly curved network, while using only straight lamellas and orthogonal joint connections.*

We anticipate to integrate this construction technology into the built environment to allow a smooth transition from a standard, vertical mullion and transom systems into a diagonal, doubly curved layout.

The design is based on a Scherk minimal surface inscribed in a cube. The module allows smooth integration into existing mullion and transom systems (A), and may be combined to create modular building envelopes (B and C) or even periodic continuous network typologies (D).

Projects Overview Page

Next Project